空间尺度上的关联性、异质性和相似性是地理学定律的基本要点。距离衰减(Distance-Decay, DD)是地理学定律和生态学理论交叉研究的一个要点，成为生物地理学研究的经典主题。在地理学定律上，这一经典主题的基本内涵是指动物、植物和微生物等各类生物群落相似性随着地理空间距离增加而呈现下降趋势。在生态学理论上，距离衰减涉及物种空间周转、种群动态同步性、群落β生物多样性、生态位分化、随机过程和扩散限制等研究范畴。然而，在数据科学上，距离衰减的定量刻画存在拟合方法和空间尺度等方面不一致，使该主题不同研究中建立的方程缺乏一定的可比性，甚至导致统计推断和结果解释存在争议。

方程是数学在科学、技术、工程和管理应用研究中的“命脉”，其在地理学和生态学研究中也不例外。围绕距离衰减定量刻画的数据科学问题，中国科学院城市环境研究所联合英国剑桥大学、印度统计研究所等单位提出了由汇编（Compilation, C）、分组（Arrangement, A）和统计（Statistics, S）等3个环节组成的分析路径（图1）。该路径英文缩写CAS恰巧与中国科学院相同，其中文名亦可喻为“中科路”。其中，汇编环节沿用了研究人员前期数据驱动研究的整合思路，并更新了原有数据集。分组环节建立了“全局样-水库群-单水库”的空间转换策略，以解析空间尺度的统计效应。统计环节则采用均值回归和分位回归对相同数据集进行对比分析。CAS路径及其以水库抗生素抗性基因（Antibiotics resistance genes, ARGs）为例建立的一系列距离衰减方程，以Distance-decay equations of antibiotic resistance genes across freshwater reservoirs为题发表在Water Research。

全局样数据分析发现：边界方程比均值方程更好地刻画相似性随距离增加呈现指数衰减关系（S = S₀e^-rD, S: 相似度, S₀: 起始相似度，e:自然常数，r: 衰减率）。水中ARGs距离衰减的边界方程和均值方程分别为S = 90.03e^-0.010D（图2a: 蓝线）和S = 14.14e^-0.021D（图2a: 黑虚线）。一方面， 在理想状态下当距离趋于零时，ARGs组成应具有100%相似度，即初始相似度为100。边界方程起始相似度为90.03更接近100，而均值方程的相似度为14.14更远离100。另一方面，衰减率在边界方程明显小于均值方程，意味着当距离作为唯一因变量时ARGs在更远距离间具有更高相似度。换句话说，边界方程可以比均值方程更好地消除未测定的变量对距离衰减关系的影响，从而更好地刻画ARGs的最大扩散潜力。沉积物ARGs边界方程和均值方程的比较，和上述水中的发现具有一致的结论，进一步证实边界方程对距离指数衰减关系的拟合能力。

水库群和全局样数据分析结果比较发现：空间尺度变换影响着距离指数衰减边界方程系数。水库群水体ARGs的边界方程是S = 86.80e^-0.007D（图3a）。该方程起始相似度（86.80）与全局样方程的90.03相差不到3%，而其衰减率（0.007）与全局样方程衰减率（0.010）相差却超过30%。水库群沉积物ARGs的边界方程为S = 91.42e^-0.024D（图3b）。沉积物ARGs距离衰减方程初始相似度在水库群和全局样两者间相差不到1%，但衰减率相差却接近50%。水库群和全局样ARGs距离指数衰减率的差异，意味着其最大扩散能力预测受空间尺度变换的影响甚大。

单水库与全局样数据分析结果比较发现：当空间尺度缩小到单个水库内部样点之间距离时，相似性随距离呈现指数衰减的规律消失了。以丹江口水库作为单个大型水库研究案例，其ARGs相似度在水体中介于26.02-94.92之间，在沉积物中介于29.41-96.13。单个大型水库水体和沉积物ARGs相似度与距离的关系处于离散型，其在上边界中随距离增加仍趋近于初始相似度（图4）。这表明，单个大型水库分析为代表的较小空间尺度内部，环境要素的异质性对ARGs相似性的影响明显大于距离形成的扩散限制。相比之下，全局样分析为代表的较大空间尺度，距离形成的扩散限制对ARGs相似性的影响明显大于环境要素的异质性。

CAS路径及其建立的多尺度距离衰减方程，为定量解析各类生物群落相似性及其形成过程与机制提供了更具可比性的方法学参考，如拟合方法、尺度变换和尺度缩减等多个视角，有助于更好地厘清生物地理学相关研究结果解释中存在的争议。视角一是，边界方程能够更真实地刻画距离衰减规律，为物种空间周转、种群动态同步性等相关研究提供了更加一致的量度。视角二是，尺度变换展示了不同系统尺度下的生物群落相似性变化及其规律，为推断生物地理要素的形成机制提供了对比性思路。视角三是，尺度缩减揭示了生物群落相似性对地理要素和环境扰动响应机制的空间依赖性，为解析尺度差异导致的生态位分化、随机过程和扩散限制等机制异同提供了路径参考。

    论文链接

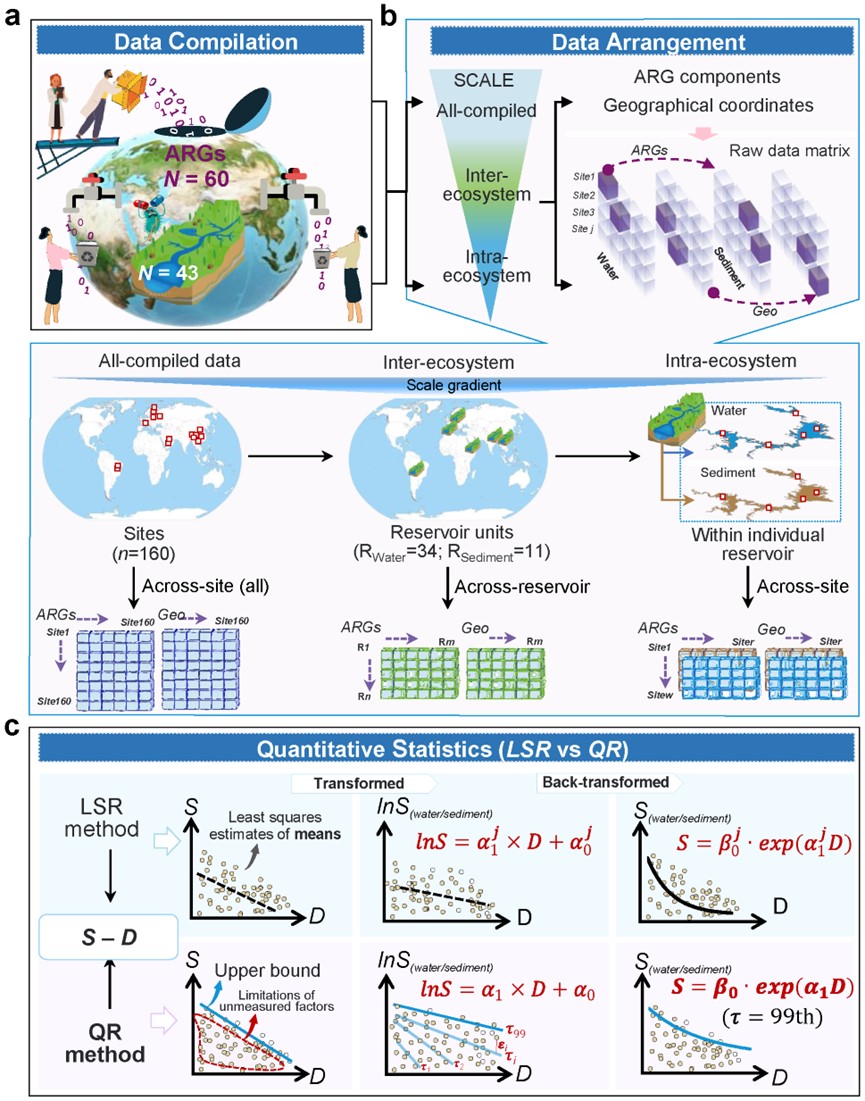
图1 边界方程刻画距离指数衰减的CAS框架

图2 全局样抗生素抗性基因距离指数衰减的边界方程及系数

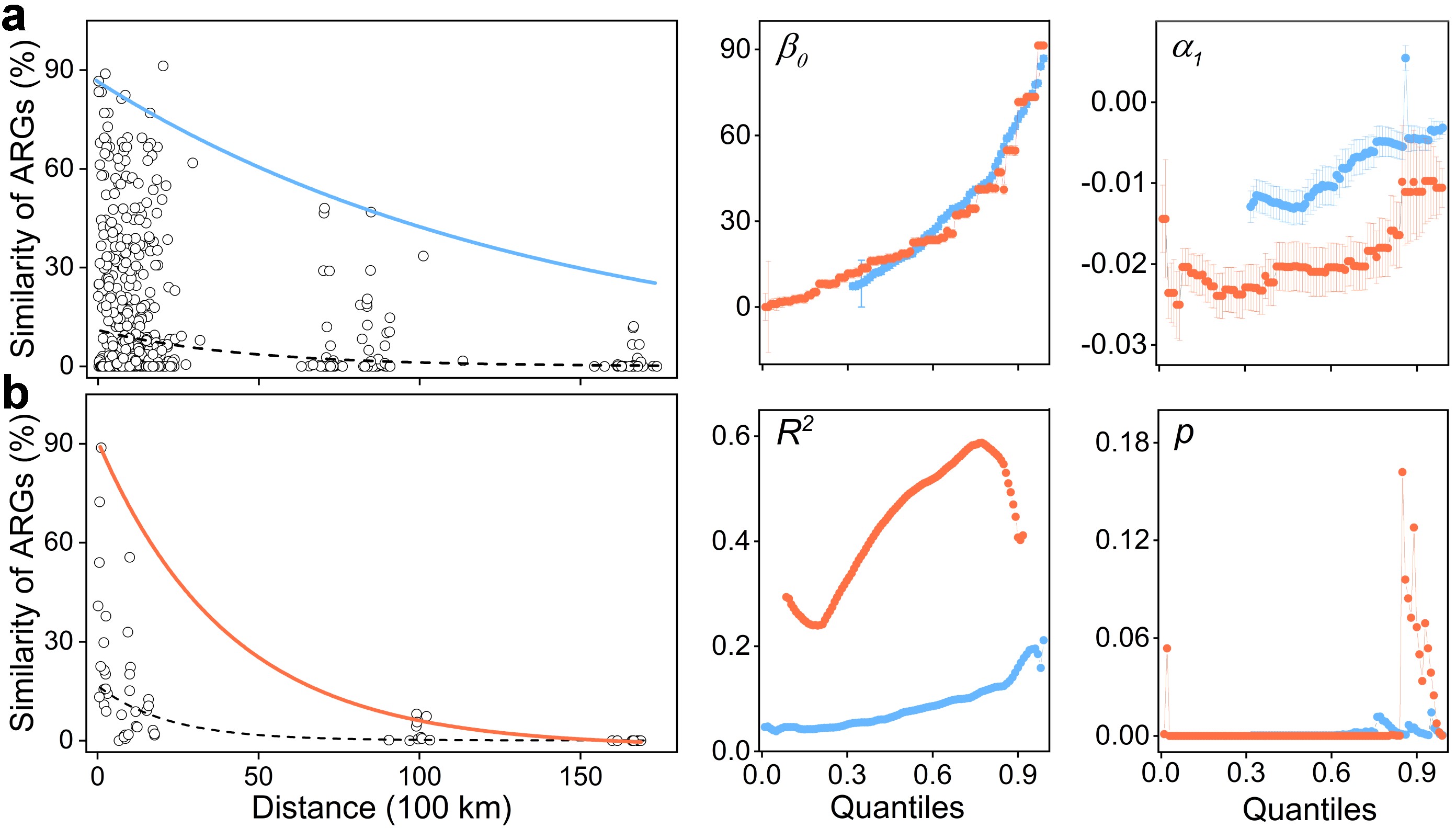
图3 水库群抗生素抗性基因距离指数衰减的边界方程及系数

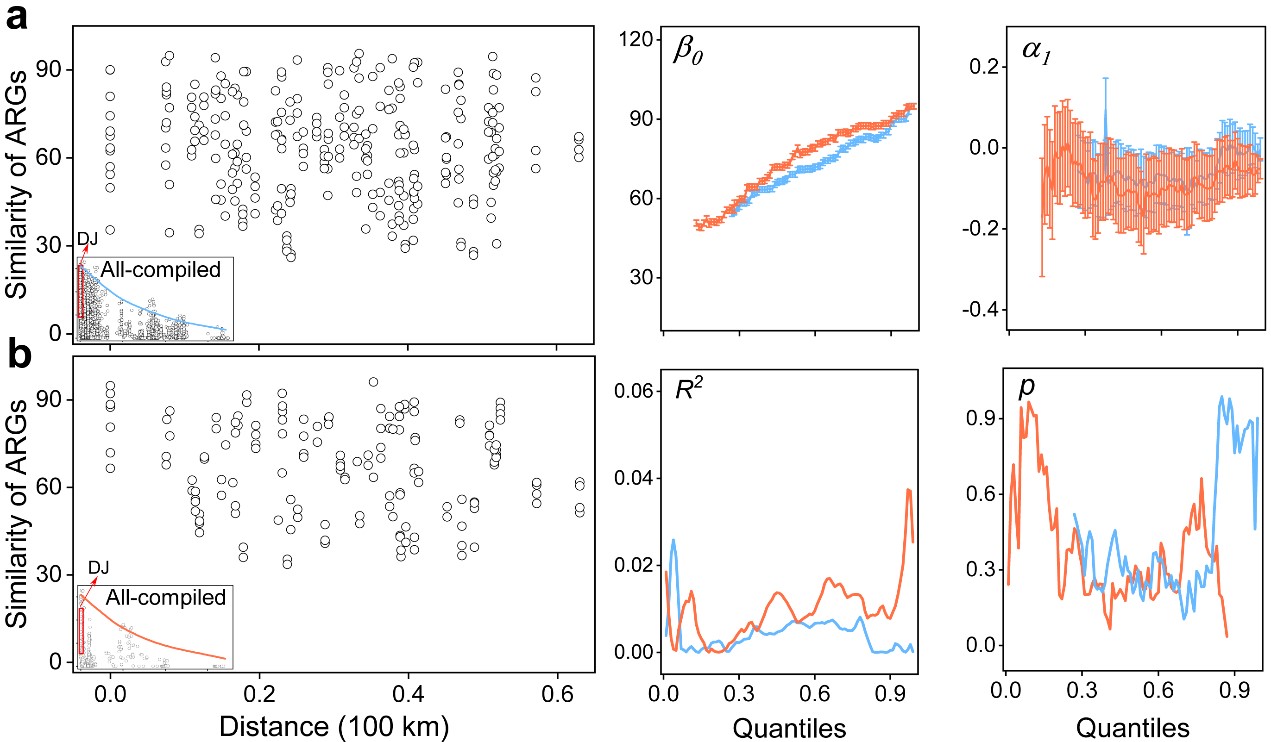
图4 单水库抗生素抗性基因距离衰减的边界方程及系数

相关资料：

1.   Guo, Z. F.; Das, K.; Boeing, W. J.; Xu, Y. Y.; Borgomeo, E.; Zhang, D.; Ao, S. C.; Yang, X. R., Distance-decay equations of antibiotic resistance genes across freshwater reservoirs. Water Res. 2024, 258, 121830.

2.   Guo, Z. F.; Boeing, W. J.; Xu, Y. Y.; Borgomeo, E.; Liu, D.; Zhu, Y. G., Data-driven discoveries on widespread contamination of freshwater reservoirs by dominant antibiotic resistance genes. Water Res. 2023, 229, 119466.

3.   Zhu, Y. G.; Gillings, M.; Simonet, P.; Stekel, D.; Banwart, S.; Penuelas, J., Human dissemination of genes and microorganisms in Earth's Critical Zone. Glob. Chang. Biol. 2018, 24, (4), 1488-1499.

4.   Das, K.; Krzywinski, M.; Altman, N., Quantile regression. Nat. Methods 2019, 16, (6), 451-452.

5.   Xu, Y. Y.; Schroth, A. W.; Rizzo, D. M., Developing a 21st Century framework for lake-specific eutrophication assessment using quantile regression. Limnol. Oceanogr.: Methods 2015, 13, (5), 237-249.

6.   Xu, Y. Y.; Schroth, A. W.; Isles, P. D. F.; Rizzo, D. M., Quantile regression improves models of lake eutrophication with implications for ecosystem-specific management. Freshw. Biol. 2015, 60, (9), 1841-1853.

7.   Koenker, R.; Bassett, G. J., Regression quantiles. Econometrica 1978, 46, 33-50.

8.   Cade, B. S.; Terrell, J. W.; Schroeder, R. L., Estimating effects of limiting factors with regression quantiles. Ecology 1999, 80, (1), 311-323.

9.   Cade, B. S.; Noon, B. R., A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, (8), 12– 420.

10. Cade, B. S.; Noon, B. R.; Flather, C. H., Quantile regression reveals hidden bias and uncertainty in habitat models. Ecology 2005, 86, (3), 786-800.

11. Qiu, Q. L. L.; Liang, Z. Y.; Xu, Y. Y.; Matsuzaki, S. S.; Komatsu, K.; Wagner, T., A statistical framework to track temporal dependence of chlorophyll–nutrient relationships with implications for lake eutrophication management. J. Hydrol. 2021, 603, 127134.

12. Liang, Z. Y.; Liu, Y.; Xu, Y. Y.; Wagner, T., A Bayesian change point quantile regression approach to enhance the understanding of shifting phytoplankton-dimethylsulfide relationships in squatic ecosystems. Water Res. 2021, 201, 117287.

13. Hanson, C. A.; Fuhrman, J. A.; Horner-Devine, M. C.; Martiny, J. B., Beyond biogeographic patterns: Processes shaping the microbial landscape. Nat. Rev. Microbiol. 2012, 10, (7), 497-506.

14. Maavara, T.; Chen, Q. W.; Van Meter, K.; Brown, L. E.; Zhang, J. Y.; Ni, J. R.; Zarfl, C., River dam impacts on biogeochemical cycling. Nat. Rev. Earth Environ. 2020, 1, (2), 103-116.

15. Nekola, J. C.; White, P. S., The distance decay of similarity in biogeography and ecology. J. Biogeogr. 1999, 26, 867-878.